Алгоритм Флойда-Уоршелла на С++
06 Июн

Задача алгоритм Флойда-Уоршелла на С++

Данный алгоритм предназначен для нахождения кратчайших расстояний между всеми вершинами взвешенного ориентированного графа.

Над матрицей выполняется некоторое количество итераций. После k-й итерации matrix[i,j] содержит значение наименьшей длины путей из вершины i в вершину j, которые не проходят через вершины с номером, большим k. Между вершинами пути i и j могут находиться только те вершины, номера которых меньше или равны k. На k-й итерации для вычисления матрицы применяется следующая формула:
matrixk[i,j]=min(matrixk-1[i,j], matrixk-1[i,k] + matrixk-1[k,j])

Входные данные: graph.txt

Исходные данные графа
Default
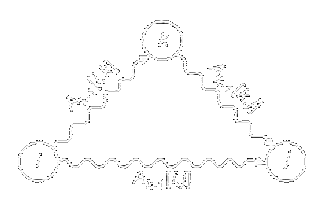
1
2
3
4
5
4
1 2 3
2 3 6
3 4 7
4 1 2

Первая строка — это количество вершин графа, дальше идут направления рёбер ориентированного графа + вес ребра (третий столбец).

 

Код:

Алгоритм Флойда-Уоршелла
C++
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
#include <iostream>
#include <fstream>
#include <algorithm>
 
void print_matrix(int** matrix, int numberOfVert, int INF) { //matrix - матрица смежности
for (int i = 0; i < numberOfVert; i++) {
for (int j = 0; j < numberOfVert; j++) {
if (matrix[i][j] == INF) { //если ячейка равна 101
std::cout << "INF" << " "; //вывести условное обозначение бесконечности
}
else { //иначе
std::cout << matrix[i][j] << " "; //вывести значение ячейки матрицы
}
}
std::cout << std::endl; //делаем перенос строки после заполнения ряда
}
}
 
 
void Floyd_Warshall(int **matrix, int numberOfVert) {
for (int k = 0; k < numberOfVert; k++) { //Пробегаемся по всем вершинам и ищем более короткий путь через вершину k
for (int i = 0; i < numberOfVert; i++) {
for (int j = 0; j < numberOfVert; j++) {
matrix[i][j] = std::min(matrix[i][j], matrix[i][k] + matrix[k][j]); //Новое значение ребра равно минимальному между старым ребром и суммой ребер
}
}
}
}
 
 
int main() {
setlocale(LC_ALL, "Russian"); //подключаем кириллицу
 
std::ifstream input_graph("graph.txt"); //открываем файл, в котором лежат данные по графу
 
int size; //переменная размерность матрицы
input_graph >> size; //заполняем размерность матрицы
 
int **massive; //двумерный динамический массив под матрицу
massive = new int* [size]; //выделяем память под ячейки массива размерностью size
for (int i = 0; i < size; i++) {
massive[i] = new int[size];
}
 
for (int i = 0; i < size; i++) { //всем ячейкам присваиваем -1
for (int j = 0; j < size; j++) { //используется как пометка для удобства расчёта
massive[i][j] = -1;
}
}
 
int v1, v2, c; //переменные для значения рёбер графа и их веса
while (!(input_graph.eof())) { //читаем файл, пока он не закончился
input_graph >> v1 >> v2 >> c; //присваиваем переменным соответствующие значения
massive[v1 - 1][v2 - 1] = c; //зеркально заполняем таблицу весов
massive[v2 - 1][v1 - 1] = c; //зеркально заполняем таблицу весов
}
input_graph.close(); //закрываем файл исходных данных графа
 
for (int i = 0; i < size; i++) { //пробегаемся по всей матрице
for (int j = 0; j < size; j++) {
if (i == j) { //если координаты ячейки совпадают
massive[i][j] = 0; //то присвоить ячейке 0, 0 - это обозначение,
//которое говорит о том, что вершина направлена сама в себя
}
else { //иначе
if (massive[i][j] == -1) { //если ячейка равна метке (-1)
massive[i][j] = 101; //то ячейке присвоить 101 (ребра из вершины нет)
}
}
}
}
 
std::ofstream matrix_size("matrix_from_size.txt"); //открываем файл с матрицей весов на запись
matrix_size << size << '\n'; //заносим первой строкой количество вершин графа
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
matrix_size << massive[i][j] << ' '; //заполняем файл значениями весов и
//делаем отступ от каждого значения
}
matrix_size << '\n'; //делаем переход на новую строку после заполнения ряда
}
matrix_size.close(); //закрываем файл
 
std::ifstream file("matrix_from_size.txt"); //открываем файл с таблицей весов на чтение
int number_of_vert; //переменная для размерности матрицы
file >> number_of_vert; //извлекаем верхушку из файла с размерностью
 
//Матрица смежности с весами ребер графа(101 - ребра нет, 0 ребро в себя)
int **matrix; //создаём двумерный динамический массив под матрицу
matrix = new int*[number_of_vert]; //выделяем память
for (int i = 0; i < number_of_vert; i++) {
matrix[i] = new int[number_of_vert];
}
 
for (int i = 0; i < number_of_vert; i++) { //Считываем матрицу весов ребер из файла
for (int j = 0; j < number_of_vert; j++) {
file >> matrix[i][j]; //в нашу матрицу
}
}
file.close(); //закрываем файл
 
Floyd_Warshall(matrix, number_of_vert); //вызываем функцию расчёта, передаём в неё нашу матрицу и размерность матрицы
 
std::ofstream result_matrix("result_matrix.txt"); //открываем файл с результатом вычислений на запись
for (int i = 0; i < number_of_vert; i++) {
for (int j = 0; j < number_of_vert; j++) {
result_matrix << matrix[i][j] << ' '; //заносим в файл значения из нашей матрицы и делаем отступ
}
result_matrix << '\n'; //делаем отступ вниз после заполнения ряда
}
result_matrix.close(); //закрываем файл с результатом
 
system("pause"); //ожидание нажатия клавиши
return 0;
}

 

Таким нехитрым образом мы познакомились с темой «Алгоритм Флойда-Уоршелла»!

Post Author: Nikulux

Похожие записи

1 thought on “Задача алгоритм Флойда-Уоршелла на С++”

    Артем

    (20.08.2020 - 21:59)

    У вас в начале говорится что граф взвешенный ориентированный, но в реализации матрица получается для неориентированного графа.
    while (!(input_graph.eof())) { //читаем файл, пока он не закончился
    input_graph >> v1 >> v2 >> c; //присваиваем переменным соответствующие значения
    massive[v1 — 1][v2 — 1] = c; //зеркально заполняем таблицу весов
    massive[v2 — 1][v1 — 1] = c; //зеркально заполняем таблицу весов (ВОТ ЭТА СТРОКА не нужна для ориентированного,
    только если граф неориентированный)
    }
    Может кому- нибуть будет полезно.

Добавить комментарий