Таким не хитрым образом мы разобрались с «таблица основных производных»!
Рубрика: Math (справочник)
Формула Ньютона-Лейбница в математике
Пусть функция непрерывна на отрезке и — одна из первообразных функции на отрезке, тогда справедлива формула Ньютона-Лейбница . Данная формула является основной формулой интегрального исчисления. Таким не хитрым образом мы познакомились с «формула Ньютона-Лейбница в математике»!
Интеграл с переменным верхним пределом в математике
Рассмотрим непрерывную функцию на отрезке функцию . Определим функцию , где . Данный интеграл носит название интеграл с переменным верхним пределом от функции . Таким не хитрым образом мы разобрались с «интеграл с переменным верхним пределом в математике»!
Теорема о среднем значении
Пусть даны две функции и такие, что: и определены и непрерывны на отрезке ; Производные и конечны на интервале ; Производные и не обращаются в ноль одновременно на интервале ; ; В таком случае существует , для которой верно: Таким не хитрым образом мы узнали о «теореме о среднем значении»!
Свойства определённого интеграла
У определённого интеграла 9 основных свойств: Значение определенного интеграла с совпадающими пределами интегрирования равно нулю. Для функции , определенной при , справедливо равенство ; При перемене верхнего и нижнего пределов интегрирования местами значение определенного интеграла меняется на противоположное. Для интегрируемой на отрезке функции выполняется ; для интегрируемых на отрезке функций и ; Постоянный множитель можно […]
Свойства интегрируемых функций в математике
Существует шесть основных свойства интегрируемых функций: Если , то по определению полагаем ; Если , то согласно определению ; Если функция интегрируема на , тогда и функция интегрируема на : ; Если функции и интегрируемы на , тогда и функция интегрируема на : ; Если функция интегрируема на . Если в конечном числе точек промежутка изменить […]
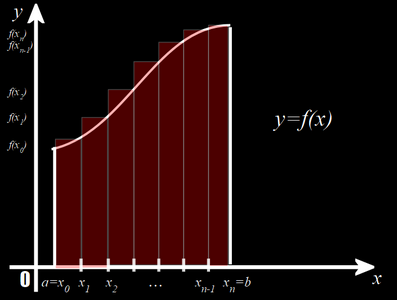
Вычисление площади криволинейной трапеции
Сумма вида равна сумме площадей прямоугольников с основаниями и высотами . Получается, данная сумма равна площади ступенчатой фигуры на рисунке. При стремлении к нулю длин всех отрезков площадь указанной ступенчатой фигуры будет стремиться к площади отмеченной на рисунке ступенчатой фигуры, лежащей под графиком функции на отрезке . Из всего вышесказанного можно сказать, что площадь криволинейной […]
Определённый интеграл в математике
Определённый интеграл — это предел интегральных сумм при стремлении диаметра разбиения к нулю, если он существует независимо от разбиения и выбора точек внутри элементарных отрезков. Обозначается следующим образом: Таким не хитрым образом мы познакомились с «определённый интеграл в математике»!
Интегрирование методом разложения
Данный метод основан на расписывании подынтегральной функции на сумму таких функций, от которых первоначальную можно найти с помощью обычных табличных интегралов. Таким не хитрым образом мы разобрались с «интегрирование методом разложения»!