Существует четыре основных свойства неопределённого интеграла Производная от результата интегрирования равна подынтегральной функции: ; Неопределенный интеграл от дифференциала функции равен сумме самой функции и произвольной константы: ; Постоянный множитель можно выносить за знак неопределенного интеграла: ; Неопределенный интеграл от суммы (разности) функций равен сумме (разности) неопределенных интегралов функций: ; Дифференциал от неопределенного интеграла равен подынтегральному […]
Первообразная — это такая функция , с промежутком /( (a; b) /), что выполняется равенство для любого из заданного промежутка. Процесс вычисления первообразной заключается в нахождении неопределённого интеграла. Неопределенныq интеграл — это всё множество первообразных функции , обозначается . Таким не хитрым образом мы разобрались с «первообразная и неопределённый интеграл»!
Алгоритм исследования функции Найти область определения функции; Исследовать поведение функции на границе области определения, найти вертикальные асимптоты; Исследовать функцию на чётность или нечётность; Найти промежутки возрастания и убывания функции, точки экстремума; Найти промежутки выпуклости и вогнутости функции, точки перегиба; Найти горизонтальные и наклонные асимптоты; Вычисление значения функции в промежуточных точках; Построение графика функции; Алгоритм построения […]
Необходимое условие перегиба Пусть график функции имеет перегиб в точке и имеет при непрерывную вторую производную, тогда выполняется равенство . Достаточное условие перегиба Пусть функция непрерывна в точке , имеет в ней касательную (допускается вертикальная) и эта функция имеет вторую производную в некоторой окрестности точки . Тогда, если в пределах этой окрестности слева и справа от […]
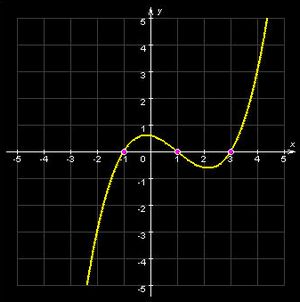
Точка перегиба — это точка, при переходе через которую функция меняет выпуклость на вогнутость или наоборот. На данном графике точкой перегиба является точка с ; Таким не хитрым образом мы разобрались с «точки перегиба графика функции в математике»!
Необходимое условие выпуклости и вогнутости функции Чтобы график был выпуклым на интервале необходимо, чтобы ; Достаточное условие выпуклости и вогнутости функции Пусть функция дважды дифференцируема, то есть имеет вторую производную, на интервале , тогда: — если для любого , то функция является вогнутой на интервале ; — если для любого , то функция является выпуклой […]
График функции , дифференцируемой на интервале , является на этом интервале выпуклым, если график этой функции в пределах интервала лежит не выше любой своей касательной. График функции , дифференцируемой на интервале , является на этом интервале вогнутым, если график этой функции в пределах интервала лежит не ниже любой своей касательной. Таким не хитрым […]
Наибольшее значение функции Наибольшее значение функции — это самое большое принимаемое значение на рассматриваемом интервале при абсциссе ; Наибольшим значением функции на промежутке называют такое значение , что для любого справедливо неравенство ; Наименьшее значение функции Наименьшее значение функции — это самое маленькое принимаемое значение на рассматриваемом интервале при абсциссе ; Наибольшим значением функции на промежутке называют […]
Необходимое условие экстремума Если точка является точкой экстремума функции , то в этой точке либо производная равна нулю, либо не существует. Экстремумы функции содержатся среди критических точек функции (точки, в которых производная функции равна нулю или не существует). Доказательство необходимого условия экстремума следует из теоремы Ферма. Достаточные условия экстремума Если производная меняет знак с минуса на плюс […]