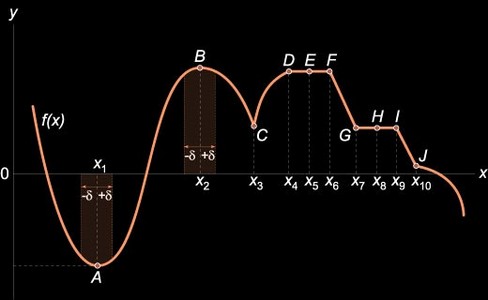
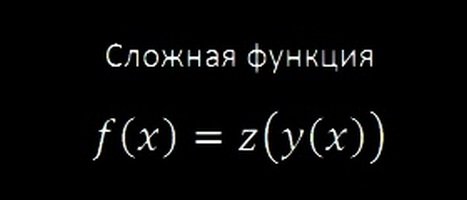Локальный максимум — это определённая точка на графике, обладающая некоторыми свойствами. Функция имеет локальный максимум в точке , если для всех точек , принадлежащих окрестности , выполняется неравенство . Если для всех точек из некоторой окрестности точки выполняется строгое неравенство , то точка является точкой строгого локального максимума. Локальный минимум — это определённая точка на графике, обладающая некоторыми свойствами. Функция имеет локальный минимум в […]
Формулировки: Если производная функции положительна для любого из интервала , то функция возрастает на ; Если производная функции отрицательна для любого из интервала , то функция убывает на ; Чтобы определить какие промежутки функции возрастают, а какие убывают необходимо: Найти область определения функции; Найти производную функции; Решить неравенства и на области определения; К полученным промежуткам добавить граничные […]
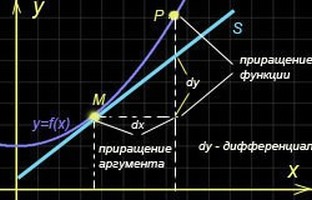
Дифференциалом функции в некоторой точке называется главная, линейная часть приращения функции. Дифференциал функции равен произведению её производной на приращение независимой переменной (аргумента) . Математически дифференциал функции в точке записывается так: или или . Таким не хитрым образом мы познакомились с «дифференциал функции в точке»!
Сложная функция — это функция, аргументом которой также является некая функция. Процесс вычисления производной сложной функции практически ничем не отличается от вычисления производной обычной функции, добавляется лишь некоторый аспект, который играет ключевую роль. Вычисление становится лишь немного сложнее, основная суть вычисления остаётся прежней. Алгоритм вычисления производной сложной функции: 1. Сначала находится производная внешней функции, аргумент при этом […]
Производная от произведения числа на функцию В данном случае справедливо равенство ; где — любое число. Словесно это значит: производная от произведения числа на функцию равна произведению этого числа на производную функции. Производная суммы функций Производная суммы функций вычисляется по следующей формуле: ; Словесно это значит: производная от суммы функций равна сумме производных этих функций Производная разности функций Производная разности функций вычисляется […]
Пусть существует некая функция , она имеет производную в точке , в таком случае выполняется следующее соотношение: . Если перенести в правую часть и перейдя к пределу, то получим следующее:. Последнее соотношение и есть искомая непрерывность функции в точке . Из дифференцируемости следует непрерывность функции. Таким не хитрым образом мы познакомились со «связью существования […]
В функции, относительно определенных точек : разность называется приращением аргумента, а разность называется приращением функции. Приращение функции обозначается греческой буквой («дельта»). и – это переменные зависящие от значений . В таком случае, корректной будет их запись такой: и . Следовательно, приращение функции — это разность . В конечном математическом виде приращение функции выглядит так: ИЛИ . Сама формула […]
Для того, чтобы понять этот самый смысл, рассмотрим следующее изображение Если тангенс угла наклона касательной линии к оси , тогда является тангенсом угла наклона той же касательной в той же точке к оси . Таким не хитрым образом мы разобрались с «геометрический смысл производной обратной функции»!
Производная обратной функции: если каждому значению у, из области изменения функции, соответствует единственное значение х, то можно говорить, что х есть функция от у. Просто функция: ; Обратная функция: ; Таким не хитрым образом мы разобрались с «Производная обратной функции»!