Локальный максимум — это определённая точка на графике, обладающая некоторыми свойствами. Функция ![]() имеет локальный максимум в точке
имеет локальный максимум в точке ![]() , если для всех точек
, если для всех точек ![]() , принадлежащих окрестности
, принадлежащих окрестности ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
Если для всех точек ![]() из некоторой окрестности точки
из некоторой окрестности точки ![]() выполняется строгое неравенство
выполняется строгое неравенство ![]() , то точка
, то точка ![]() является точкой строгого локального максимума.
является точкой строгого локального максимума.
Локальный минимум — это определённая точка на графике, обладающая некоторыми свойствами. Функция ![]() имеет локальный минимум в точке
имеет локальный минимум в точке ![]() , если для всех точек
, если для всех точек ![]() , принадлежащих окрестности
, принадлежащих окрестности ![]() , выполняется неравенство
, выполняется неравенство ![]() .
.
Если для всех точек ![]() из некоторой окрестности точки
из некоторой окрестности точки ![]() выполняется строгое неравенство
выполняется строгое неравенство ![]() , то точка
, то точка ![]() является точкой строгого локального минимума.
является точкой строгого локального минимума.
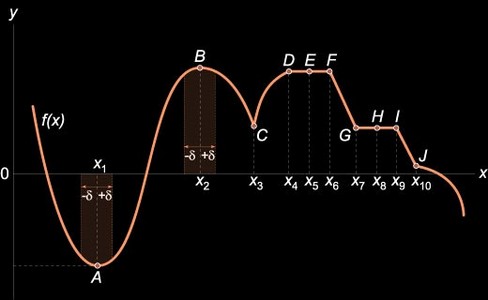
- Точка
 − строгий минимум;
− строгий минимум; - Точка
 − нестрогий максимум;
− нестрогий максимум; - Точка
 − нестрогий максимум или минимум;
− нестрогий максимум или минимум; - Точка
 − нестрогий максимум;
− нестрогий максимум; - Точка
 − нестрогий минимум;
− нестрогий минимум; - Точка
 − нестрогий максимум или минимум;
− нестрогий максимум или минимум; - Точка
 − нестрогий максимум;
− нестрогий максимум; - Точка
 − экстремума нет.
− экстремума нет.
Таким не хитрым образом мы познакомились с «локальные максимум и минимум функции в математике»!