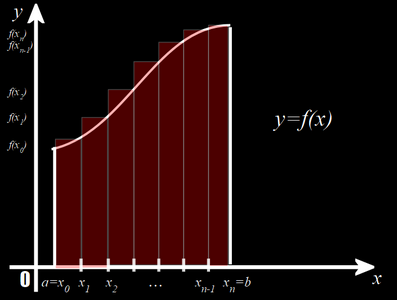
Вычисление площади криволинейной трапеции
21 Июн

Вычисление площади криволинейной трапеции

Сумма вида S \approx f(x_1) \Delta x_1 + f(x_2) \Delta x_2 + ... + f(x_n) \Delta x_nравна сумме площадей прямоугольников с основаниями \Delta x_k и высотами f(x_k) . Получается, данная сумма равна площади ступенчатой фигуры на рисунке.
При стремлении к нулю длин всех отрезков \Delta x_k площадь указанной ступенчатой фигуры будет стремиться к площади отмеченной на рисунке ступенчатой фигуры, лежащей под графиком функции f(x) на отрезке (a; b).

Из всего вышесказанного можно сказать, что площадь криволинейной трапеции можно вычислить по следующей формуле: S = \lim_{\lambda \to 0} \sum^{k}_{n=1} f(x_n) \Delta x_n = \int^b_a f(x)dx;

 

Таким не хитрым образом мы разобрались с «вычисление площади криволинейной трапеции»!

Post Author: Nikulux

Похожие записи

Добавить комментарий